არაევკლიდური გეომეტრია
არაევკლიდური გეომეტრია — პირდაპირი გაგებით – ნებისმიერი გეომეტრიული სისტემა, რომელიც განსხვავდება ევკლიდური გეომეტრიისაგან, თუმცა ტრადიციულად ტერმინში "არაევკლიდური გეომეტრია" გულისხმობენ ძირითადად ორ გეომეტრიულ სისტემას: ლობაჩევსკის გეომეტრიასა და სფერულ გეომეტრიას.
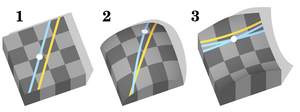
არაევკლიდურ გეომეტრიაში 5 ძირითადი პოსტულატიდან მე-5 (პარელელური წრფეების აქსიომა) ჩანაცვლებულია სხვით. მაგალითად ლობაჩევსკის გეომეტრიაში იგი ნაცვლდება აქსიომით: მოცემულ წერტილზე მოცემული წრფის პარალელურად გაივლება არანეკლებ ორი წრფისა. ეს შესააძლებელია თუ დავუშვებთ რომ სივრცე სფერული ფორმისსაა, ხოლო ნებისმიერი წრფე წრეწირს წრამოადგენს. თუ მოცემულ წრფედ სფეროს ეკვატორულ წრეწირს ავიღებთ, მაშინ ცხადი იქნება, რომ ნებისმიერ წერტილზე, რომელიც ამ წრფეს არ ეკუთვნის, შეიძლება უამრევი წრეწირის აგება , ისე რომ არც ერთი მათგანი მოცემილ წრეწირს არ გადაკვეთს. მოცემული სფერული სივრცის დიამეტრს უსასრულებისკენ მივასწრაფებთ, ანუ ʀ→∞ , მაშინ მოცემულ წრეწირთა რადიუსები უსასრულოდ გაიზრდება, შედეგად მივიღებტ წრფეებს.
1733 წელს იტალიელმა მათემატიკოსმა ჯიროლამო საკერიმ გაატარა მეხუთე პასტულატის სრულიად ორიგინალურ პრინციპზე დამყარებული ღრმა გამოკვლევა. საკერის იდეა მდგომარეობდა მეხუთე პასტულატის საწინააღმდეგო დებულებით ჩანაცვლებაში. ამგვარად, მეხუთე პასტულატის მართებულობა დამტკიცებული იქნებოდა მისი საწინააღმდეგო დებულობის მცდარობით.
XIX საუკუნის პირველ ნახევარში საკერის მიერ გადებულ გზას გაუყვა ერთდროულად სამი მათემატიკოსი: გაუსი, ნიკოლაი ლობაჩევსკი და იანოშ ბოიაი. მაგრამ მათი მიზანი სხვა იყო - მათ სურდათ არა არაევკლიდური გეომეტრიის შეუძლებლობის დამტკიცება, არამედ პირიქით — ალტერნატიული გეომეტრიის აგება და რეალურ სამყაროში მისი მიზნის გაგება. იმ დროს ამგვარი იდეა სრულიად ერეტიკული იყო. მანამდე არც ერთ მეცნიერს ეჭვი არ შეჰპარვია, რომ ფიზიკური სივრცე ევკლიდური იყო.
პირველი იყო გაუსი. მას ამ თემასთან დაკავშირებით ნამუშევრები არ გამოუქვეყნებია, მაგრამ მისი ჩანაწერები და წერილები მოწმობს მის ღრმა ცოდნაზე არაევკლიდურ გეომეტრიაში.
ლობაჩევსკის ნამუშევართან „გეომეტრიული გამოკვლევები პარალელურობის თეორიაზე“ გაცნობის შემდეგ, გაუსი აქტიურად მონაწილეობს და მოითხოვს რუსი მათემატიკოსის წევრ-კორესპონდეტად გაწევრიანებას გეტინგენის სამეფო საზოგადოებაში (რაც მოხდა კიდევაც 1842 წელს).
ლობაჩევსკიმ და ბოიაიმ გაუსზე მეტი სიმამაცე გამოიჩინეს და თითქმის ერთდროულად (ლობაჩევსკიმ 1826-29 წლებში; ბოიამ 1831-32 წლებში), ერთმანეთისგან დამოუკიდებლად, გამოაქვეყნეს ექსპოზიცია იმისა, რასაც ახლა ლობაჩევსკის გეომეტრია ჰქვია. ნიკოლაი ლობაჩევსკი ახალი გეომეტრიის შესწავლაში ყველაზე შორს წავიდა, ამიტომაც ახლა ეს გეომეტრია მის სახელს ატარებს.