ბრეზენჰემის ალგორითმი
ბრეზენჰამის სეგმენტის აგების ალგორითმი არის ბრეზენჰამის მიერ ჩამოყალიბებული ალგორითმი 1962 წელს, მაშინ როდესაც ის მუშაობდა IBM-ის ინფორმატიკის ლაბორატორიაში და ცდილობდა მოეძებნა მეთოდი რომლითაც შეძლებდა ტექსტის კურსორის მართვას. ეს ალგორითმი წარმოდგენილი იყო 1963 წლის ACM-ის კონვენციაზე. შემდეგ კი გამოქვეყნდა 1965 წლის ჟურნალ IBM Systems Journal.
ალგორითმი განსაზღვრავს დასახული გეგმის პუნქტებს, რომლებიც უნდა დაიხაზოს რათა შეადგინოს სეგმენტის მარჯვენა ნაწილის მიახლოება მოცემულ ორ პუნქტს შორის. ეს ალგორითმი ხშირად გამოიყენება კომპიუტერის ეკრანის მარჯვენა მხარეზე სურათის ხაზის გასავლებად ან გამოსახულების ასაგებად. ის განიხილება როგორც ერთ-ერთი პირველად აღმოჩენილი ალგორითმი გამოსახულების სინთეზის სფეროში.
გამოყენება
რედაქტირებაგამოთვლის პრინციპი ფართოდ არის დოკუმენტირებული და იგი გამოიყენება ნებისმიერი კონუსური მრუდის, ან ბეზიერის კონუსის გამოსასახად.შესაძლებელია აგრეთვე მისი მორგება მრუდის მიახლოებასთან რომლის სასრული გაშლაა მხოლოდ ცნობილი(რომლისთვისაც მხოლოდ დაბალი ხარისხს ავიღებთ).
ალგორითმი აგრეთვე გამოიყენება 2 განზომილებიანზე დიდ სივრცეში მრუდის და ფართობის გამოსაანგარიშებლად. ორ განზომილებაშიც კი ამ ალგორითმით შესაძლებელია მრუდის და ფუნქციის სასრული წერტილების გამოთვლა, ორ პუნქტს შორის დაშვებული შეცდომების გათვალისწინებით. იგი აგრეთვე ფართოდ გამოყენებულია სურათების დასამუშავებლად და შუალედური ფერების ინტერპოლაციისთვის.
პირველი ბაიტში შემავალი მონაცებესი საბაზო ალგორითმის ახსნა
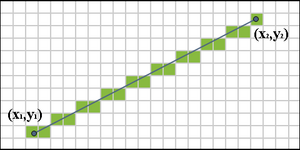
რედაქტირებამონაკვეთი იხატება ორ წერტილს შორის (x1, y1) და (x2, y2), სადაც ამ წყვილში მითითებულია სვეტი და სტრიქონი, შესაბამისად, რომელთა ნომრები იზრდება მარჯვნივ და ქვევით. დავუშვათ რომ ჩვენი ხაზი მიდის ქვევით და მარჯვნივ, ამასთან ჰორიზონტალური მანძილი x2-x1 აღემატება ვერტიკალურს y2-y1, ხაზის დახრა ჰორიზონტალურად ნაკლებია 45°-ზე. ჩვენი მიზანია ყოველი x კოლონისთვის რომელიც მოთავსებულია x0 და x1 შორის განვსაზღვროთ რომელი y სვეტია ყველაზე ახლოს ხაზთან, და დავხატოთ (x,y) წერტილი.
ორდინატთა განსაზღვრა
რედაქტირებაორ წერტილს შორის ხაზის საერთო ფორმულა:
- . (1)
რადგანაც ჩვენ ვიცით კოლონა -x, მაშინ y ხაზი გამოდის დამრგვალებული მთელის შემდეგ მნიშვნელობამდე:
- . (2)
მაგრამ ამ გამოსახულები ზუსტი მნიშვნელობის გამოთვლა უაზრობაა, საკმარისია ავღნიშნოთ რომ y იზრდება y0-იდან და თითოეულ ბიჯზე ჩვენ x-ს ვუმატებთ 1-ს და y-ს დახრის მნიშვნელობას
რომლის გამოთვლა წინასწარ არის შესაძლებელი. მეტიც, თითოეულ ბიჯზე ჩვენ ან y-ის მნიშვნელობას ვინახავთ, ანდა მას 1-ით ვზრდით. ყოველთვის როდესაც ჩვენ x-ს სიდიდეს ვზრდით ჩვენ ამავდროულად ზემოთ მოყვანილი s დახრის სიდიდის შეცდომის მნიშვნელობასაც ვზრდით. თუ შეცდომა აღემატება 0.5, ხაზი უფრო მიუახლოვდება შემდეგ y-ს, ამიტომ ჩვენ y-ს ვზრდით 1-ით, რითიც შეცდომის მნიშვნელობის 1-ით შემცირებას ვიწვევთ.
პროცედურა შემდეგნაირიამ დავუშვათ რომ tracerPixel(x, y) არის გრაფიკული პრიმიტივი რომელიც გამოსახავს x სტრიქონის და y სვეტის პიქსელებს; გამოხატულია ფსევდო კოდში, საბაზო ალგორითმი კი შემდეგია:
procédure tracerSegment(entier x1, entier y1, entier x2, entier y2) est
déclarer entier x, y, dx, dy ;
déclarer rationnel e, e(1,0), e(0,1) ; // მცდარი მნიშვნელობა და ნაზრდი
dy ← y2 - y1 ;
dx ← x2 - x1 ;
y ← y1 ; // საწყისი მდგომარეობა
e ← 0,0 ; // საწყისი მცდარი მნიშვნელობა
e(1,0) ← dy / dx ;
e(0,1) ← -1.0 ;
pour x variant de x1 jusqu’à x2 par incrément de 1 faire
tracerPixel(x, y) ;
si (e ← e + e(1,0)) ≥ 0,5 alors // იმავე რიგის მომდევნო პიქსელის მცდარი მნიშვნელობა
y ← y + 1 ; // სასურველია უფრო მაღალი რიგის მომდევნო პიქსელი ამორჩევა
e ← e + e(0,1) ; // აზუსტებს დაჩვებულ შეცდომას ახალ სტრიქონში
fin si ;
fin pour ;
fin procédure ;
მთელ რიცხვებზე გამოთვლების ჩასატარებელი ალგორითმის გაუმჯობესება
რედაქტირებაამ ალგორითმის მთავარი პრობლემა შემდეგში მდგომარეობას: კომპიუტერის მიკროპროცესორი შედარებით ნელია მცოცავ მძიმიან რიცხვებზე(და ზემოთ მოყვანილი მცოცავ მძიმიანი რიცხვების რაციონალური რიცხვების სახით წარმოდგენა e და e(1,0)-სთვის გაცილებით რთულია და ითხოვს ინსტრუქციათა დიდ რაოდენობას); ხოლო მთელ რიცხვებთან მუშაობა უფრო ზუსტ და სწრაფ გამოთვლის საშუალებას მოგვცემდა. პირველი ხერხი იმაში მდგომარეობს რომ თავიდანვე შეგვიძლია შევცვალოთ e e-0,5-ით, რაც ორი რაციონალური რიცხვის შედარების მაგივრად შესაძლებლობას გვაძლევს შეცდომის ნიშანი შევამოწმოთ, ეს საშუალებას გვაძლევს ზუსტად გავიგოთ რომელი ორი პიქსელია განთავსებული პარალელური მარჯვენა მხარის ქვევით, რომელთა ორდინატები გაიზარდა 0,5-ით და შევცვალოთ ის.
procédure tracerSegment(entier x1, entier y1, entier x2, entier y2) est
déclarer entier x, y, dx, dy ;
déclarer' rationnel e, e(1,0), e(0,1) ; // მცდარი მნიშვნელობის და ნაზრდი'
dy ← y2 - y1 ;
dx ← x2 - x1 ;
y ← y1 ; // საწყისი მდგომარეობა
e ← -0,5 ; // საწყისი მცდარი მნიშვნელობა
e(1,0) ← dy / dx ;
e(0,1) ← -1.0 ;
pour x variant de x1 jusqu’à x2 par incrément de 1 faire
tracerPixel(x, y) ;
si (e ← e + e(1,0)) ≥ 0 alors // იმავე რიგის მომდევნო პიქსელის მცდარი მნიშვნელობა
y ← y + 1 ; // სასურველია უფრო მაღალი რიგის მომდევნო პიქსელი ამორჩევა
e ← e + e(0,1) ; // აზუსტებს დაჩვებულ შეცდომას ახალ სტრიქონში
fin si ;
fin pour ;
fin procédure ;
შემდეგ ყოველი რაციონალური რიცხვის dx-ით გაზრდისას გამოთვლა აღარ ითხოვს რაციონალური რიცხვების გაზრდას. ამავდროულად e=-0,5×dy საწყისი მნიშვნელობა ჯერ არ არის მთელი რიცხვი, მაშინაც კი თუ მისი ნაზრდი მთელი რიცხვია.
procédure tracerSegment(entier x1, entier y1, entier x2, entier y2) est
déclarer entier x, y, dx, dy ;
déclarer rationnel e ; // შეცდომის მნიშვნელობა
déclarer entier e(1,0), e(0,1) ; // ნაზრდი
dy ← y2 - y1 ;
dx ← x2 - x1 ;
y ← y1 ; // საწყისი მდგომარეობა
e ← -0,5 × dx ; // საწყისი მცდარი მნიშვნელობა
e(1,0) ← dy ;
e(0,1) ← -dx ;
pour x variant de x1 jusqu’à x2 par incrément de 1 faire
tracerPixel(x, y) ;
si (e ← e + e(1,0)) ≥ 0 alors // იმავე რიგის მომდევნო პიქსელის მცდარი მნიშვნელობა
y ← y + 1 ; // სასურველია უფრო მაღალი რიგის მომდევნო პიქსელი ამორჩევა
e ← e + e(0,1) ; // აზუსტებს დაჩვებულ შეცდომას ახალ სტრიქონში
fin si ;
fin pour ;
fin procédure ;
თუმცა e-ს გაორმაგება(და მისი ნაზრდების მნიშვნელობებისა),არ ცვლის არაფერს მისი ნიშნის ტესტირებაში: e წარმოადგენს მანძილს მარჯვენა ზუსტ ორდინატიასდმი, რომელიც გაზრდილია 0,5-ით, ეს მანძილი გაზრილი იქნა რა მუდმივი დადებითი ფაქტორით 2×dy (რომელიც არ ცვლის ტესტირებული შეცდომის მნიშვნელობას). დახრის მნიშვნელობა, რომელიც გამოიყენება როგორც e-ს ნაზრდი გაზრდილი აგრეთვე იგივე ფაქტორით გახდება 2×dy, მისი საწყისი მნიშვნელობა კი -dx, მეორე პირობითი დეკრემენტი გახდება 2×dx(რომელიც შეიძლება წინასწარ გამოვთვალოთ). ალგორითმი კი გახდება შემდეგნაირი:
procédure tracerSegment(entier x1, entier y1, entier x2, entier y2) est
déclarer entier x, y, dx, dy ;
déclarer entier e ; // შეცდომის მნიშვნელობა
déclarer entier e(1,0), e(0,1) ; // ნაზრდი
dy ← y2 - y1 ;
dx ← x2 - x1 ;
y ← y1 ; // საწყისი მნიშვნელობა
e ← -dx ; // საწყისი მცდარი მნიშვნელობა
e(1,0) ← dy × 2 ;
e(0,1) ← -dx × 2;
pour x variant de x1 jusqu’à x2 par incrément de 1 faire
tracerPixel(x, y) ;
si (e ← e + e(1,0)) ≥ 0 alors // იმავე რიგის მომდევნო პიქსელის მცდარი მნიშვნელობა
y ← y + 1 ; // სასურველია უფრო მაღალი რიგის მომდევნო პიქსელი ამორჩევა
e ← e + e(0,1) ; // აზუსტებს დაჩვებულ შეცდომას ახალ სტრიქონში
fin si ;
fin pour ;
fin procédure ;
ცვლადი სიდიდეების შემცირება და გამარტივება
რედაქტირებასაბოლოოდ შესაძლებელია e-ს ნიშნის შეცვლა მისი მოპირდაპირე ნიშნის ტესტირებით, შემდეგ ცვალებადი სიდიდეების რაოდენობის შემცირებით, იმის კონსტატირებით რომ ზემოთ ნახსენები dx და dy აღარ გამოიყენება, როგორც კი თავდაპირველი შეცდომა და ნაზრდი გამოთვლილი არიან; საკმარისია აგრეთვე ნაზრდის და დეკრემენტის ნიშნის შეცვლა:
procédure tracerSegment(entier x1, entier y1, entier x2, entier y2) est
déclarer entier dx, dy ;
déclarer entier e ; // შეცდომის მნიშვნელობა
dy ← ( y2 - y1) × 2 ; // e(1,0)
dx ← (e ← x2 - x1) × 2 ; // -e(0,1)
tant que x1 < x2 faire
tracerPixel(x1, y1) ;
x1 ← x1 + 1 ; // მომდევნო პიქსელების კოლონა
si (e ← e - dy) ≤ 0 alors // იმავე რიგის მომდევნო პიქსელის მცდარი მნიშვნელობა
y1 ← y1 + 1 ; // სასურველია უფრო მაღალი რიგის მომდევნო პიქსელი ამორჩევა
e ← e + dx ; // აზუსტებს დაჩვებულ შეცდომას ახალ სტრიქონში
fin si ;
fin faire ;
// Le pixel final (x1, y1) n’est pas tracé.
fin procédure ;
ეს ალგორითმი ოპტიმალურია და საკმარისია იმისათის რომ დავხაზოთ ნებისმიერი დახრილი და დიაგონალური ჰორიზონტალური ვექტორი პირველ ბაიტში, ზრდად სვეტებსა და კოლონებში. ავღნიშნოთ რომ თუ პროგრამირების ენა საშუალებას გვაძლევს ორი ლოკალური გამოცხადებული ცვლადი x და y შეიძლება ჩანაცვლებული იყვნენ x1 და y1 ცვლადების პარამეტრების გამოყენებით. ეს შემთხვევა ზევითაა განხილული.
და მაინც უნდა აღინიშნოს რომ ზემოთ ნახსენებ ალგორითმში, e-ს ტესტირებული ნიშანი უდრიდეს ან არ უდრიდეს ნულს. თუ ვირჩევთ დიაგონალურ გადაადგილებას მომდევნოდ ორი პუნქტი ყოველთვის მიღებული იქნება დიაგონალური გადაადგილებით; ხოლო თუ ვირჩევთ ჰორიზონტალურ გადაადგილებას, მომდევნო ორი პუნქტი ყოველთვის მიღებული იქნება ჰორიზონტალური გადაადგილებით.
განზოგადებული ოპტიმიზირებული ალგორითმი
რედაქტირებასაბაზო ალგორითმის განზოგადება მიღებულია, ნებისმიერი მიმართულებით გავლებული ვექტორების მიერ შექმნილი წირის მარტივი სიმეტრიით.
აქ მოყვანილი ალგორითმი განვითარებულია და ოპტიმიზირებულია 8 ბაიტში. იმისთვის რომ დავრწმუნდეთ რომ ერთი და იგივე გამოსახულების ელემენტები ყოველთვის აგებული იქნება ორი ერთი და იგივე მაგრამ საპირისპირო მიმართულების მქონე ვექტორისთვის, შევაბრუნოთ სასაზღვრო პირობები, სადაც დიაგონალური გადაადგილება პირდაპირი გადაადგილების ტოლია, ამოვირჩიოთ დიაგონალი როდესაც ვექტორი უფრო მეტად ორიენტირებულია მარცხნივ(კლებადი აბსცისისკენ) ვიდრე მაჯვნივ(ზრდადი აბსცისისკენ), როგორც აქ მოყვანილ შემთხვევაში:
procédure tracerSegment(entier x1, entier y1, entier x2, entier y2) est
déclarer entier dx, dy;
si (dx ← x2 - x1) ≠ 0 alors
si dx > 0 alors
si (dy ← y2 - y1) ≠ 0 alors
si dy > 0 alors
// მრუდი ვექტორი პირველ მეოთხედში
si dx ≥ dy alors
// დიაგონალური ვექტორი ან მრუდი ჰორიზონტალურთან მიახლოებულიმ პირველ ბაიტში ' déclarer entier e ;
dx ← (e ← dx) × 2 ; dy ← dy × 2 ; // e არის დადებითი
boucler sans fin // ჰორიზონტალური გადაადგილება
tracePixel(x1, y1) ;
interrompre boucle si (x1 ← x1 + 1) = x2 ;
si (e ← e - dy) < 0 alors
y1 ← y1 + 1 ; // დიაგონალური გადაადგილება'
e ← e + dx ;
fin si ;
fin boucle ;
sinon
// ვერტიკალუღტან მიახლოებული მრუდი ვექტორი, მეორე ბაიტში
déclarer entier e ;
dy ← (e ← dy) × 2 ; dx ← dx × 2 ; // e არის დადებითი
boucler sans fin // ვერტიკალური გადაადგილება
tracePixel(x1, y1) ;
interrompre boucle si (y1 ← y1 + 1) = y2 ;
si (e ← e - dx) < 0 alors
x1 ← x1 + 1 ; // დიაგონალური გადაადგილება
e ← e + dy ;
fin si ;
fin boucle ;
fin si ;
sinon // dy < 0 (et dx > 0)
// მრუდი ვექტორი მეოთხე მეოთხედში
si dx ≥ -dy alors
// დიაგონალური ვექტორი ან მრუდი ჰორიზონტალურთან მიახლოებული, მერვე ბაიტში
déclarer entier e ;
dx ← (e ← dx) × 2 ; dy ← dy × 2 ; // e არის დადებითი
boucler sans fin // ჰორიზონტალური გადაადგილება
tracePixel(x1, y1) ;
interrompre boucle si (x1 ← x1 + 1) = x2 ;
si (e ← e + dy) < 0 alors
y1 ← y1 - 1 ; // დიაგონალური გადაადგილება
e ← e + dx ;
fin si ;
fin boucle ;
sinon // ვერტიკქლურთან მიახლოებული მრუდი ვექტორი მეშვიდე ბაიტში
déclarer entier e ;
dy ← (e ← dy) × 2 ; dx ← dx × 2 ; // e არის უარყოფითი
boucler sans fin // ვერტიკალური გადაადგილება
tracePixel(x1, y1) ;
interrompre boucle si (y1 ← y1 - 1) = y2 ;
si (e ← e + dx) > 0 alors
x1 ← x1 + 1 ; // დიაგონალური გადაადგილება
e ← e + dy ;
fin si ;
fin boucle ;
fin si ;
fin si ;
sinon // dy = 0 (et dx > 0)
// მარჯვნივ მიმართული ჰორიზონტალური ვექტორი
répéter
tracePixel(x1, y1) ;
jusqu’à ce que (x1 ← x1 + 1) = x2 ;
fin si ;
sinon // dx < 0
si (dy ← y2 - y1) ≠ 0 alors
si dy > 0 alors
// მრუდი ვექტორი მეორე მეოთხედში
si -dx ≥ dy alors
// მრუდი ვექტორი ან ჰორიზონტალურთან მიახლოებული მრუდი, მეოთხე ბაიტში
déclarer entier e ;
dx ← (e ← dx) × 2 ; dy ← dy × 2 ; // e არის უარყოფითი
boucler sans fin // ჰორიზონტალური გადაადგილება
tracePixel(x1, y1) ;
interrompre boucle si (x1 ← x1 - 1) = x2 ;
si (e ← e + dy) ≥ 0 alors
y1 ← y1 + 1 ; // დიაგონალური გადაადგილება
e ← e + dx ;
fin si ;
fin boucle ;
sinon
// ჰორიზონტალურთან მიახლოებული მრუდი ვექტორი, მესამე ბაიტში
déclarer entier e ;
dy ← (e ← dy) × 2 ; dx ← dx × 2 ; // e არის დადებითი
boucler sans fin // ვერტიკალური გადაადგილება
tracePixel(x1, y1) ;
interrompre boucle si (y1 ← y1 + 1) = y2 ;
si (e ← e + dx) ≤ 0 alors
x1 ← x1 - 1 ; // დიაგონალური გადაადგილება
e ← e + dy ;
fin si ;
fin boucle ;
fin si ;
sinon // dy < 0 (et dx < 0)
// მრუდი ვექტორი მესამე მეოთხედში
si dx ≤ dy alors
// დიაგონალური ვექტორი ან ჰორიზონტალურთან მიახლოებული მრუდი, მეხუთე ბაიტში
déclarer entier e ;
dx ← (e ← dx) × 2 ; dy ← dy × 2 ; // e არის უარყოფითი
boucler sans fin // ჰორიზონტალური გადაადგილება
tracePixel(x1, y1) ;
interrompre boucle si (x1 ← x1 - 1) = x2 ;
si (e ← e - dy) ≥ 0 alors
y1 ← y1 - 1 ; // დიაგონალური გადაადგილება
e ← e + dx ;
fin si ;
fin boucle ;
sinon // ვერტიკალურთან მიახლოებული მრუდი ვექტორი, მეექვსე ბაიტში
déclarer entier e ;
dy ← (e ← dy) × 2 ; dx ← dx × 2 ; // e არის უარყოფითი
boucler sans fin // ვერტიკალური გადაადგილება
tracePixel(x1, y1) ;
interrompre boucle si (y1 ← y1 - 1) = y2 ;
si (e ← e - dx) ≥ 0 alors
x1 ← x1 - 1 ; // დიაგონალური გადაადგილება
e ← e + dy ;
fin si ;
fin boucle ;
fin si ;
fin si ;
sinon // dy = 0 (et dx < 0)
// მარჯვნივ მიმართული ჰორიზონტალური ვექტორი
répéter
tracePixel(x1, y1) ;
jusqu’à ce que (x1 ← x1 - 1) = x2 ;
fin si ;
fin si ;
sinon // dx = 0
si (dy ← y2 - y1) ≠ 0 alors
si dy > 0 alors
// ვერტიკალურად ზრდადი ვექტორი
répéter
tracePixel(x1, y1) ;
jusqu’à ce que (y1 ← y1 + 1) = y2 ;
sinon // dy < 0 (et dx = 0)
// ვერტიკალურად კლებადი ვექტორი
répéter
tracePixel(x1, y1) ;
jusqu’à ce que (y1 ← y1 - 1) = y2 ;
fin si ;
fin si ;
fin si ;
// საბოლოო პიხელები (x2, y2) არ არის გავლებული.
fin procédure ;
საყურადღებოა:
- გრაფიკული პრიმიტივი tracePixel(x1, y1) თავს იყრის, რომ გაივლოს ჰორიზონტალური სეგმენტი შიდა ბუკლში(პირველი ბაიტის შემთხვევაში) ან ვერტიკალური(მეორე ბაიტის შემთხვევაში) და ისინი ამასთანავე თავს იყრიან ერთ გამოძახებაძე.(საკმარისია მხოლოდ, დავითვალოთ პასაჟების რაოდენობა შიდა ბუკლში და ავაგოთ ჰორიზონტალური სეგმენტი ამ ბუკლის გამოსასვლელზე)